Windenergieanlagen verursachen durch eine Reihe verschiedener Mechanismen Schall. Wenn man eine Windenergieanlage hört, dann hört man meist die Strömungsgeräusche die direkt an den Flügel entstehen. Vielleicht hört man auch Generator und Getriebegeräusche.
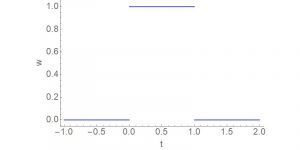
Darüber hinaus verursachen Windenergieanlagen Infraschall, der durch das Vorbeiziehen der Rotorblätter vor dem Mast verursacht wird. Dieser Effekt ist nicht Windenergieanlagen spezifisch, sondern verursacht bei jedem Axiallüfter Schall, und mit einem Druckminimum oder Maximum jedes Mal wenn ein Flügelblatt an einem Steg vorbeizieht. Hat ein Elektrogerät einen Axiallüfter, dann entsteht das hörbare Lüftergeräusch hauptsächlich durch diese Druckschwankungen.
Im Gegensatz zu einem kleinen Elektrolüfter dreht sich die eine Windenergieanlage sehr langsam. Die Frequenz des entstehenden Geräuschs hängt von der Drehzahl ab, und wird durch die langsamen Umdrehungen der Windenergieanlage aus dem hörbaren Bereich des Schalls in den tiefen Infraschallbereich verschoben.
Angenommen, eine Windenergieanlage dreht sich mit 14 Umdrehungen pro Minute. Da sie drei Rotorblätter hat, zieht 3*14 Mal pro Minute ein Rotorblatt am Mast vorbei. Als Frequenz ausgedrückt ist das 3*14 pro Minute = 3*14/60 pro Sekunde = 0,7 pro Sekunde = 0,7 Hz.
Bei einer Frequenz von 0,7 Hz ist die Periodenlänge 1/0,7 Sekunden, also ca. 1,4 Sekunden. Das ist die Zeit nach der sich das Signal wiederholt, die sich auch daraus ergibt, dass in 60 Sekunden 3*14 Mal ein Rotorblatt am vorbeizieht, und 60/(3*14) ≈1,4 ist.
Bei Wind herrscht eine ständige Strömung um den Mast der Windenergieanlage. Jedes Mal, wenn ein Rotorblatt am Mast vorbeizieht, entsteht eine Störung in dieser Strömung. Diese Störung führt zu einer Luftdruckschwankung, die sich als Schall von der Windenergieanlage ausbreitet. In diesem Fall Infraschall, weil die Frequenz sehr niedrig ist.
Die von der WEA ausgehende Schalldruckwelle breitet sich mit Schallgeschwindigkeit aus, das sind ca. 340 m/s. Es dauert ca. 1,4 Sekunden, bis sich das Signal wiederholt, in dieser Zeit hat sich die Welle um 340 m/s * 1,4s ≈470 m. Diese Strecke, nach der sich die Welle wiederholt, wird als Wellenlänge bezeichnet.
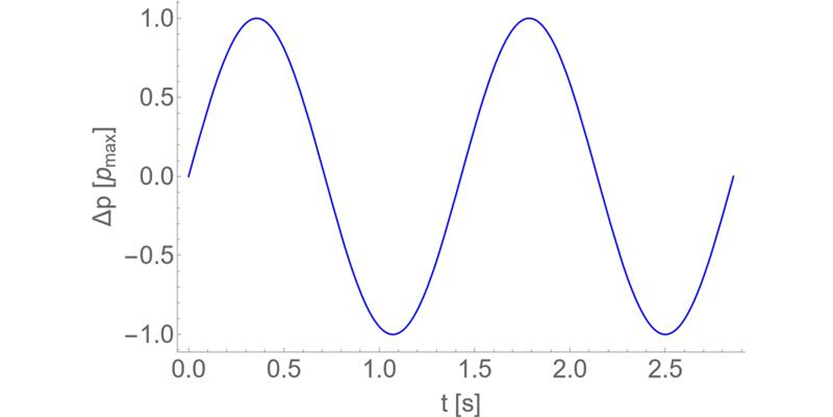
In Abbildung 1 ist eingezeichnet, wie der Schalldruckverlauf an einem Immissionspunkt aussähe, wenn die erzeugte Schalldruckwelle wirklich nur ein Sinus mit einer Frequenz von 0,7 Hz wäre. Eine Spektrum – also eine Darstellung der Frequenzanteile dieses Signals – hätte nur einen einzelnen Beitrag bei 0,7 Hz. In einer üblichen Darstellung wäre das eine scharfe Linie bei 0,7 Hz.
In der Realität gibt es wenig Grund anzunehmen, dass das Passieren des Masts durch Rotorblätter Druckschwankungen verursacht, die genau wie ein Sinus aussehen. Der tatsächliche Schalldruckverlauf kann also auch eine andere Form annehmen. Wenn man aber annimmt, dass der Wind konstant ist und sich die Windenergieanlage mit konstanter Drehzahl bewegt, dann müssen diese Signal periodisch sein. Egal welche Form der Schalldruckverlauf hat, er muss sich alle 1/0,7 Sekunden wiederholen. Und das ist gleichbedeutend damit, dass sich der Schalldruckzeitverlauf aus Sinussen mit Frequenzen zusammensetzen muss, die ganzzahlige Vielfache der Grundfrequenz von 0,7 Hz sind.
In den folgenden Abbildungen ist ein Beispiel dargestellt, wie sich (für den idealisierten, streng periodischen Fall) ein Schalldruckzeitverlauf aus den Sinussen von Grundton und Harmonischen zusammensetzen kann. Links jeweils der Schalldruckzeitverlauf, und rechts das zugehörige Spektrum. Im Spektrum sind nur die Beiträge von Grundton und Harmonischen als Linie zu sehen, weil aufgrund der Periodizität alle anderen Beiträge Schalldruck Null sind, bzw. in Dezibel bei minus Unendlich liegen.
Auch wenn das Schalldruckzeitsignal so aussieht, als wären es eher „Pulse“ als harmonische Sinusschwingungen, sieht man doch, dass sich das Signal aus Sinussen zusammensetzen lässt.
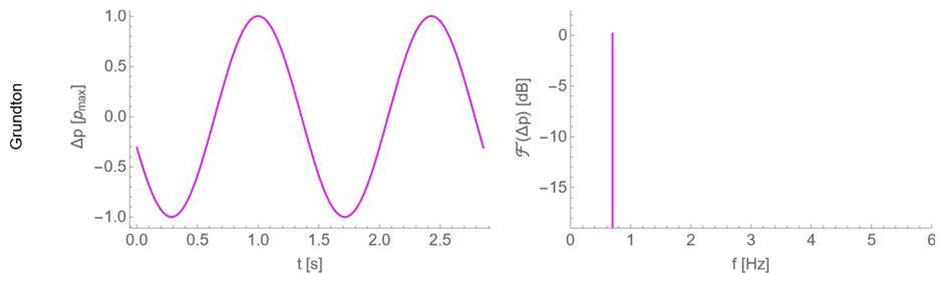
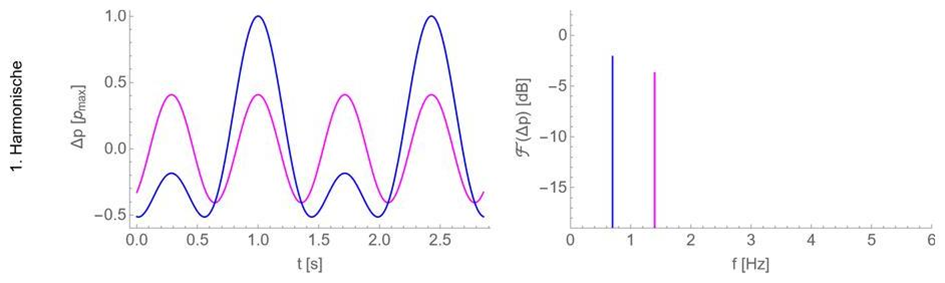
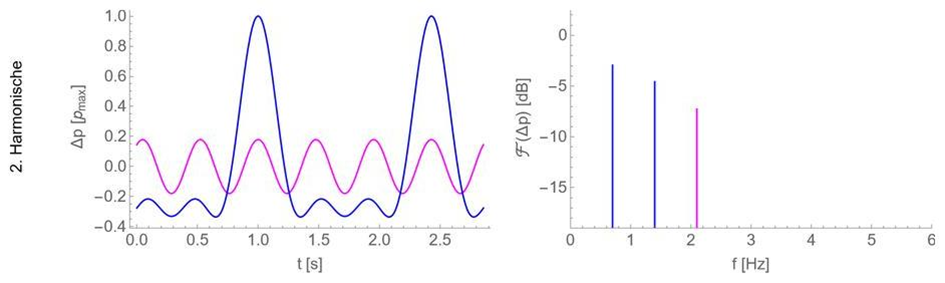
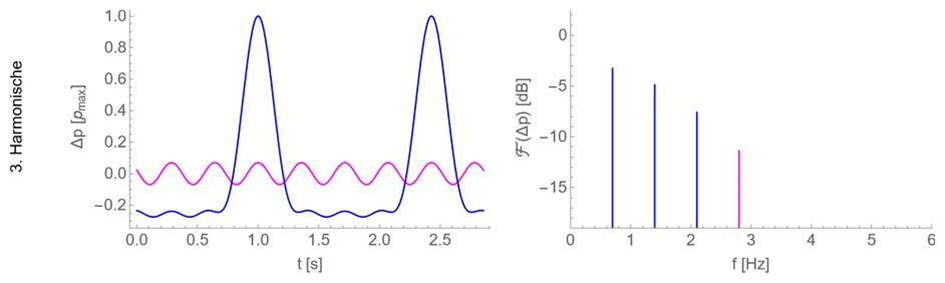
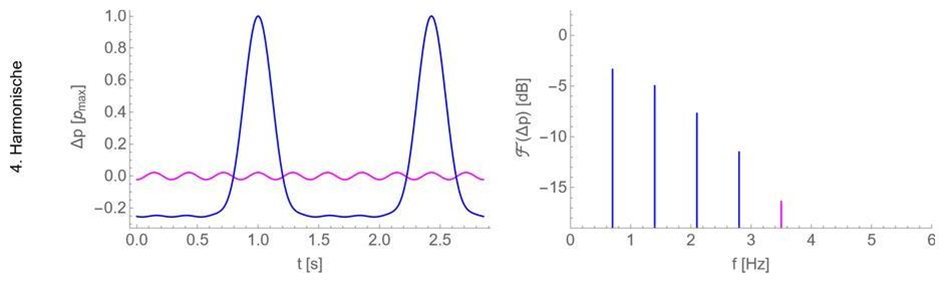
Auch wenn das Schalldruckzeitsignal so aussieht, als wären es eher „Pulse“ als harmonische Sinusschwingungen, sieht man doch, dass sich das Signal aus Sinussen zusammensetzen lässt.
In Abbildung 3 ist ein Spektrum aus einer Immissionsmessung im Freien dargestellt. Deutlich erkennbar sind die durch WEA verursachten Einzellinien. Der Grundton liegt bei 0,624 Hz, die weiteren Linien bei ganzzahligen Vielfachen.
Im Gegensatz zum fiktiven Beispiel oben ist nicht die Linie beim Grundton die Linie mit dem größten Beitrag. Das liegt zu einem Teil daran, dass die Messtechnik zu tiefen Frequenzen unempfindlicher wird, und etwas kleinere Pegel misst, als tatsächlich vorhanden sind. Aber auch wenn die Messtechnik perfekt linear wäre, würde der größte Beitrag nicht vom Grundton kommen. Das liegt daran, dass die Wellenlängen beim Grundton und der ersten Harmonischen extrem lang werden.
Vielleicht ist das von Lautsprechern bekannt: Ein Tieftöner muss größer dimensioniert sein als ein Hochtöner. Je tiefer das erzeugte Geräusch sein soll, um so größer muss der Lautsprecher sein.
In diesem Fall ist die Wellenlänge des Grundtons bei 550m. Die Druckschwankung wird zwischen Mast und Rotorblatt erzeugt, effektiv auf einer Länger kleiner als 50m. Das heißt, die Wellenlänge (und auch ein Viertel der Wellenlänge) ist deutlich größer als die Länge der Quelle, und deshalb kann die Quelle eine so tiefe Frequenz nur eingeschränkt abstrahlen – egal wie die physikalischen Prozesse im Detail aussehen.
Generalisiert heißt das:
- Egal wie langsam eine WEA dreht, sie kann nicht beliebig tiefe Frequenzen mit hohen Pegeln abstrahlen.
- Je größer die WEA werden, bzw. je länger die Rotorblätter werden, um so mehr können extrem tiefe Frequenzen abgestrahlt werden.
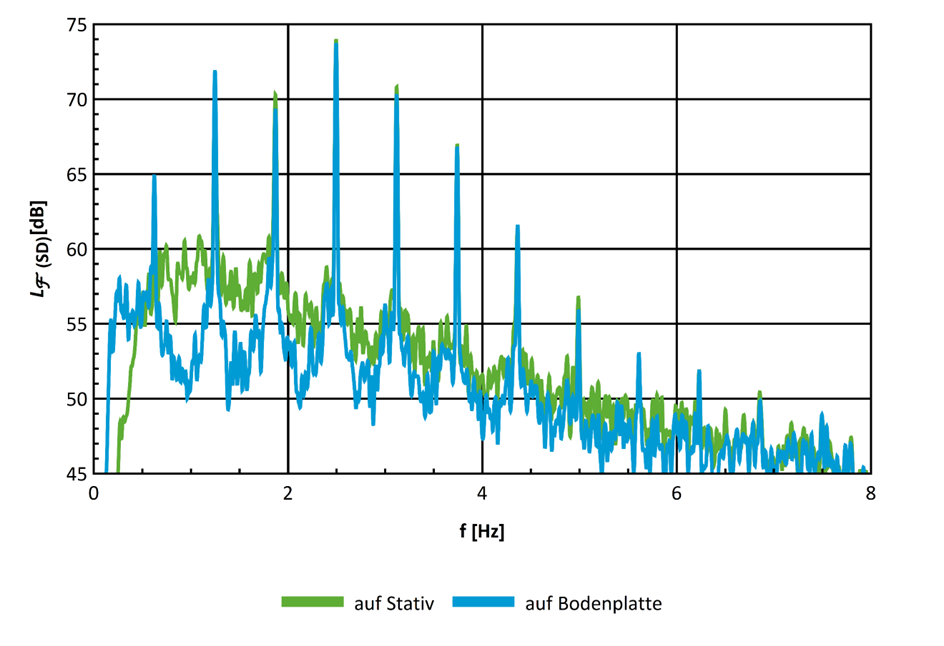
Abbildung 3 Spektrum einer Immissionsmessung[1]
In diesem Fall wurde zeitgleich mit einem Mikrophon auf einem Stativ und einem zweiten Mikrophon auf einer Bodenplatte gemessen. Neben den Linien ist im Spektrum ein breiter Untergrund zu sehen, bei den Messungen auf Stativ bei etwas höheren Pegeln als bei der Messung auf der Bodenplatte. Dieser breitbandige Anteil im Spektrum wird im Wesentlichen durch Wind verursacht. Weil der Wind mit der Höhe zunimmt, sind diese Windbeiträge auf der Bodenplatte kleiner als auf dem Stativ.
Man kann in diesem Spektrum also erkennen, dass es einen breitbandigen Teil gibt, der durch Wind verursacht wird. Und es gibt scharfe Linien, die durch die WEA verursacht werden. In diesem Fall ist das eine relativ klare Sache.
Das Spektrum einer WEA sieht aber nicht notwendigerweise aus wie in der Abbildung oben. So scharfe Linien gibt es nämlich nur, wenn der zugrunde liegende Prozess sehr periodisch ist. Tatsächlich ist es aber so, dass sich das Vorbeiziehen der Rotorblätter am Mast zwar streng periodisch wiederholt, aber der Wind kann jedes Mal ein kleines bisschen anders sein. Kleine Änderungen im Wind führen dazu, dass sich die Linien im Spektrum verbreitern. Werden die Änderungen im Wind größer, dann verbreitern sich die Linien immer weiter, und sind irgendwann nicht mehr als Linien erkennbar.
[1] Geräuschwirkungen bei der Nutzung von Windenergie an Land | Umweltbundesamt